Supervised Learning: Neural Networks
This is the 4th in a series of class notes as I go through the Georgia Tech/Udacity Machine Learning course. The class textbook is Machine Learning by Tom Mitchell.
Neurons and Perceptrons
Behold, a Neuron. You hopefully have a few of these.

Information travels from the cell body in “spike trains” down the axon and causes synapse excitation on other neurons. So Neurons are a complicated computational unit. They can be tuned or trained through a learning process to fire on different things, and other neurons can fire on that, and so on. Brains are a tight wad of 100 billion neurons, or a natural neural network, if you will, all firing one after the other to make conscious and unconscious decisions.
Artificial neurons (aka Perceptrons) try to emulate this:

A vector of inputs are fed into the neuron, which multiplies them by a vector of weights and sums them up. If the sum is above a certain firing threshold, the neuron is activated and fires an output of 1. If it is not activated, it has an output of 0.
How Powerful is a Perceptron Unit?
It can represent half planes in multiple dimensions.
- A simple perceptron with 2 binary inputs and equal weights with a threshold higher than either weight can represent the AND logical operator.
- If the threshold is equal to either weight, it represents the OR logical operator.
- Similarly you can also make NOT.
For more you should really check this and related videos:
To make XOR, you have to combine perceptrons by applying a strong negative weight on an AND perceptron together with an OR perceptron:
Perceptron Training
Instead of setting weights by hand like we have been doing, we should automate that. The two ways to do this are:
- Perceptron Rule
- Gradient descent/delta rule
Perceptron Rule
Setting a single unit so it matches a training set.

The weight change equals the difference of the target (what we want it to be, either 0 or 1) and the output (what the network currently spits out, also 0 or 1), multiplied by the input and the learning rate (which is a small number, like 0.01).
In other words, if the output of the perceptron is correct, there will be no change to the weight. But if the output is wrong, the weight will be moved a small step in the direction of the difference in target vs output.
If a dataset is linearly separable, the perceptron rule will find the right plane to separate them. That’s cool!

However, if the dataset is not linearly separable (and we have no way to tell ahead of time, especially in multiple dimensions), the Perceptron Rule gets stuck in an infinite loop. We need something more robust.
Gradient Descent
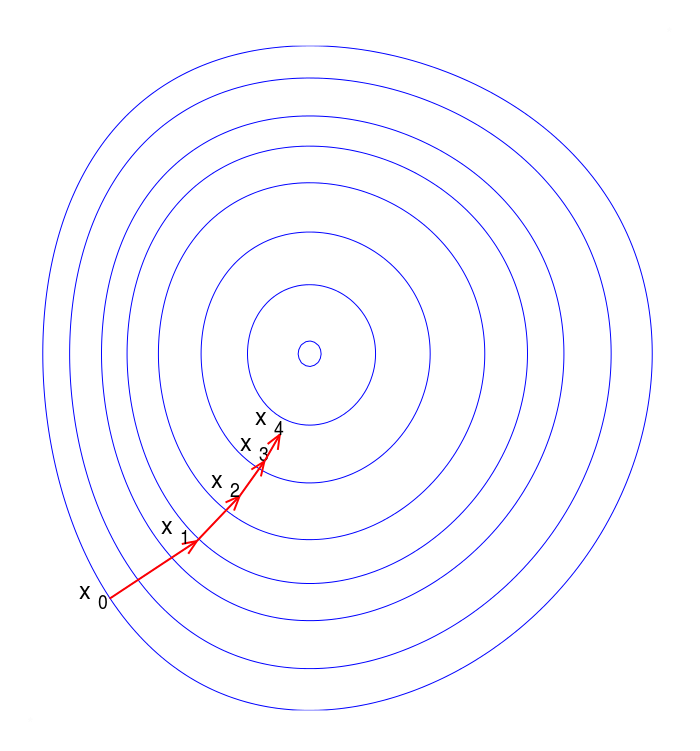
In contrast to the Perceptron Rule, Gradient Descent throws out the idea of a threshold. It uses the same mechanism of incremental updating but uses partial derivatives instead. In fact, the formulas end up looking very similar:

The Perceptron Rule guarantees finite convergence if the data is linearly separable. Gradient Descent is more robust, but can only converge toward a local optimum.
The reason we can’t use gradient descent on the Perceptron Rule’s y_hat is because the activation threshold behavior is a discontinuous function that is undifferentiable. What if we changed that to a function that kinda sorta looks like the activation function but that is differentiable?
Sigmoid function
The sigmoid function in equation form looks simple enough and has a very appealing chart form:

If you make it narrow enough it looks like the binary activation function! and if you take its derivative, it turns out that it is sigmoid(a) multiplied by (1 - sigmoid(a)):
Which is a very neat closed form solution for gradient descent purposes.
Networking Perceptrons
Having a network of differentiable perceptrons is very useful. Despite having multiple hidden layers between input and output, we can backpropagate the errors to update weights in the entire network!
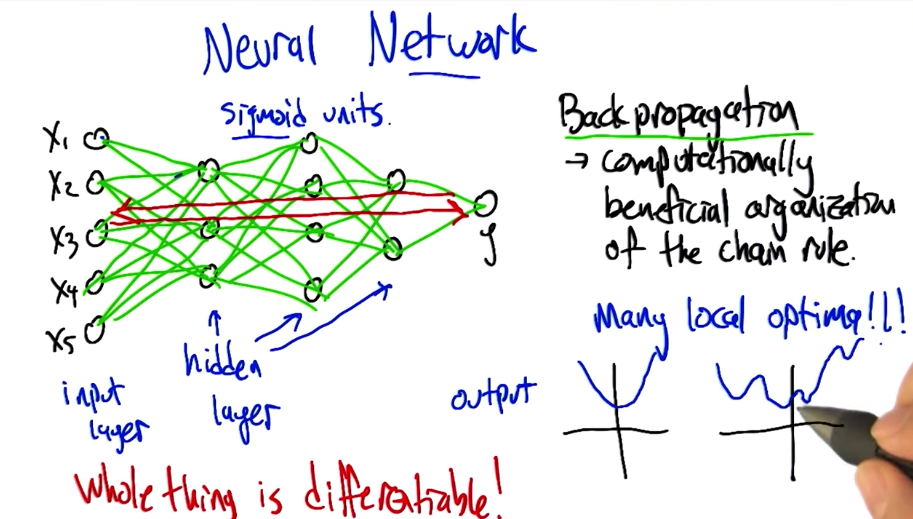
Optimizing Weights
In gradient descent you can often get stuck in local optima.
To break this, you can:
- use a momentum term
- use randomized optimization
- penalize complexity (similar to what we discussed previously with regression/decision tree overfitting)
- more nodes
- more layers
- large numbers (nonobvious!)
Bias in Neural nets
Restriction bias (the set of hypotheses we will consider):
- Perceptrons: Half planes
- Sigmoid units: Much more complex - they can represent boolean, continuous (one hidden layer), and arbitrary functions (two hidden layers).
So Neural nets dont have much restriction bias at all. It also means that it is very possible to overfit. To guard against this, we also use cross-validation and look for divergences in error to identify overfitting.
Preference bias (the algorithm’s preference for one representation over another):
We have specified everything for gradient descent except for how it is initialized! Most often we use small random values. This is because large weights let us represent arbitrarily complex functions and that is not good.
Read More
More is available in the PDF summary here.
Next in our series
Hopefully that was a good introduction to Neural Networks. I am planning more primers and would love your feedback and questions on:
- Overview
- Supervised Learning
- Unsupervised Learning
- Randomized Optimization
- Information Theory
- Clustering - week of Feb 25
- Feature Selection - week of Mar 4
- Feature Transformation - week of Mar 11
- Reinforcement Learning
- Markov Decision Processes - week of Mar 25
- “True” RL - week of Apr 1
- Game Theory - week of Apr 15
